Die Geometrie entstand aus der praktischen Notwendigkeit, ein begrenzte Ressource, nämlich flaches Ackerland, in regelmäßigen Abständen und möglichst konfliktfrei aufzuteilen. Nicht zufällig steht die Wiege der Geometrie in Ägypten: Dieses schon früh von Menschen besiedelte Land besteht zum größten Teil aus Wüste. Allein entlang des Nils zieht sich ein schmaler Grünstreifen durch das Land. Hier ein Bild aus dem All:
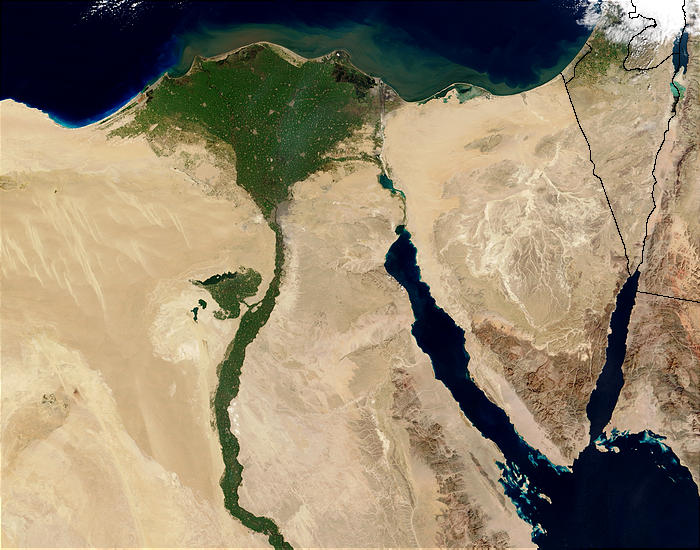
Dieser bis zu 30 km breite Streifen ist im Wesentlichen flach und wurde seit Urzeiten, bis zum Bau des Assuan-Staudamms in den 60-er Jahren des vergangenen Jahrhunderts, jährlich für etwa 3 Monate vom Nil überschwemmt. Nach den Überschwemmungen wurde das dadurch urbar gemachte Land beackert, bis zur nächsten Überschwemmung. Es ergab sich folglich die Notwendigkeit, das Land jedes Jahr neu in Parzellen aufzuteilen. Um solche Landverteilungen möglichst schnell und reibungslos durchzuführen, brauchte man ausgebildete Leute, die mit einfachsten Mitteln Parzellen abmessen konnten. Man benötigte nicht mehr als Seile und Pflöcke: Ein gespanntes Seile beschreibt eine Strecke oder Gerade. Bindet man das eine Ende eines Seils an einen Pflock, so kann man mit dem anderen Ende in der Hand einen Kreis abschreiten.
Damit sind wesentliche Ingredienzien der antiken Geometrie gegeben: Konstruktionen mit Zirkel und Lineal auf einer ebenen Fläche, sowie möglichst wenige und einfach zu vermittelnde Regeln, mit denen man auch komplizierte Landvermessungen meistern kann. Wie diese Regeln aussahen, und wie sie gelehrt wurden, kann man in den Büchern des Euklid, der sie etwa 300 v. Chr. aufschrieb, nachlesen: Definition, Satz und Beweis. Die Elemente des Euklid bestehen aus 13 Büchern. Neun davon behandeln Geometrie. Die Elemente basieren auf einer schon bei ihrer Entstehung jahrtausendealten mathematik-pädagogischen Erfahrung. Es ist somit kein Wunder, dass selbst in der heutigen Zeit die elementare Geometrie vielfach noch direkt nach den Büchern des Euklid gelehrt wird.
Tatsächlich sind die ältesten bekannten Texte über Geometrie etwa 4000 Jahre alt: Der Papyrus Moskau 4676 (ca. 1850 v. Chr.) enthält 25 Rechenaufgaben, darunter 4 Aufgaben geometrischer Natur, unter anderm eine zur Berechnung des Volumens eines Pyramidenstumpfes. Es gibt auf dem Papyrus offenbar Korrekturbemerkungen. Aus dieser Tatsache und vielen anderen altägyptischen und babylonischen Relikten kann man schlussfolgern, dass elementare geometrische Erkenntnisse wie der Satz des Pythagoras in der einen oder anderen Form schon über ein Jahrtausend vor Pythagoras (ca. 570 - 510 v. Chr.) gelehrt wurden.
Den zweiten großen Schub in ihrer Entwicklung erhielt die Geometrie aus dem Projekt der Vermessung der Erde. Zeitlich ist dies etwa Ende des 18. und Anfang des 19. Jahrhundert einzuordnen. Man brauchte möglichst exakt die Umgebung beschreibende Karten, sowohl für die Seefahrt, als auch für militärische Zwecke. Letztere sind unmittelbar einsichtig: Mit Kanonen weit entfernte Ziele zu treffen benötigt exaktere Hilfsmittel als allein gutes Augenmaß. In der Seefahrt waren durch Kompasse, Sextanten und präzise Uhren die technischen Hilfsmittel so weit entwickelt, dass auch hier hohe Ansprüche an möglichst präzise Karten gestellt wurden. Je exakter man Karten machen will, desto größer wird das damit einhergehende mathematische Problem: Wie kann man krumme Objekte, wie die Erde, auf flaches Papier abbilden? Aus einer Karte möchte man Entfernungen, Richtungen und Winkel ablesen können. Unter welchen Umständen und auf welche Weise geht das? Lassen sich immer längentreue oder winkeltreue Karten, oder gar beides, zeichnen?
Mit solchen Fragen musste sich Carl Friedrich Gauß auseinandersetzen, als er von seinem Dienstherrn, dem König von Hannover, Großbritannien und Irland, beauftragt wurde, das Königreich Hannover zu vermessen. Aus dieser Beschäftigung entstand das Theorema Egregium, eine Aussage über die Krümmung von Flächen.
Das behandelte Phänomen lässt sich anschaulich erläutern. Flächen krümmen sich nämlich auf drei unterschiedliche Weisen:

Eierschalen sind sphärisch gekrümmt. Will man Eierschalen auf einem ebenen Tisch flach ausbreiten, so brechen sie. Lokal besitzen sie weniger Oberfläche als der Tisch.

Diese Blüte ist hyperbolisch. Eine Satteldecke wäre ein anderes Beispiel. Will man eine Satteldecke auf einem ebenen Tisch flach ausbreiten, so wirft sie Falten. Lokal besitzt eine hyperbolische Fläche mehr Oberfläche als der Tisch.
Papierseiten sind flach. Sie mögen vielleicht gebogen in den umgebenden Raum eingebettet sein, und als krumm erscheinen. Man kann sie aber immer auf einem ebenen Tisch ausbreiten, ohne dass sie zerreißen oder Falten werfen. Lokal besitzen sie genauso viel Oberfläche wie der Tisch.
Die Vermessung der Erde Ende des 18. und Anfang des 19. Jahrhunderts bildete so den Anstoß zur Entwicklung der Differentialgeometrie. Für das theoretische Verständnis grundlegend war der am 08. Oktober 1827 in lateinischer Sprache veröffentlichte Aufsatz Disquisitiones generales circa superficies curvas, zu deutsch Allgemeine Flächentheorie, von Carl Friedrich Gauß. Die nächste Sternstunde der Geometrie datiert auf den 10. Juni 1854, an dem im Beisein des 77-jährigen Carl Friedrich Gauß der damals 27-jährige Bernhard Riemann seinen Habilitationsvortrag zum Thema Über die Hypothesen, welche der Geometrie zu Grunde liegen hielt. In diesem Habilitationsvortrag skizzierte Bernhard Riemann einem mehrheitlich nicht mathematisch gebildeten Publikum im Wesentlichen ohne Formeln das ganze Spektrum dessen, was ich Ihnen in diesem Semester beibringen will. Wir starten mit dem Konzept der Mannigfaltigkeit und enden mit der Konstruktion des Riemannschen Krümmungstensors.
