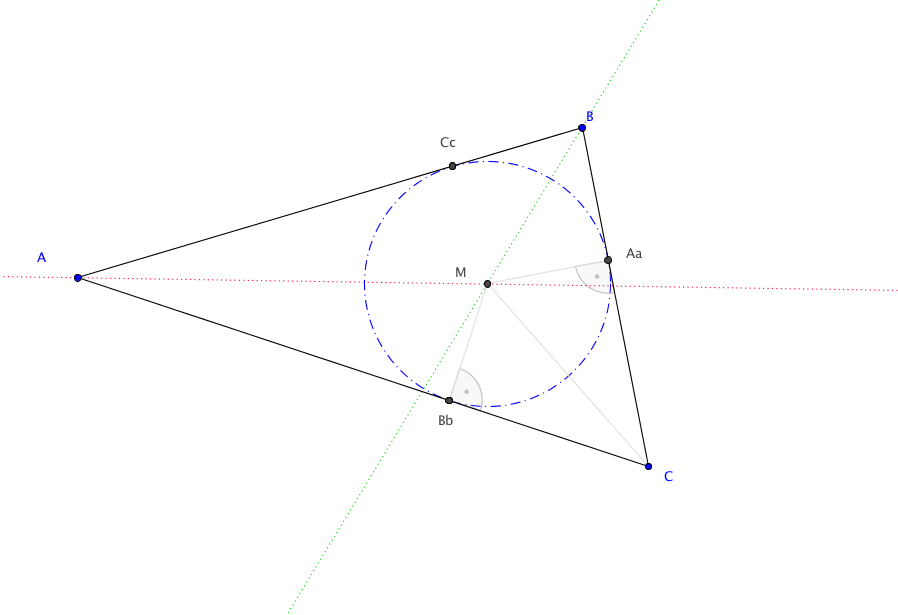
Proposition 3.7. Die Mittelsenkrechten der Seiten $\overline{AB},\overline{BC}$ und $\overline{CA}$ eines nicht ausgearteten Dreiecks schneiden sich im Mittelpunkt des Umkreises.
Beweis. Es seien $g$ und $h$ die Mittelsenkrechten zweier der drei Seiten, sagen wir von $\overline{AB}$ und $\overline{CA}$. Sind $g$ und $h$ parallel, so sind die Geraden $AB$ und $AC$ ebenfalls parallel und haben $A$ als gemeinsamen Punkt. Damit gilt $AB=CA$ und folglich ist das Dreieck $ABC$ ausgeartet im Widerspruch zur Voraussetzung. Somit schneiden sich die Geraden $g$ und $h$ in einem Punkt $M$. Die Spiegelung $s_g$ bildet die Strecke $\overline{AM}$ auf die Strecke $\overline{BM}$ ab, die Spiegelung $s_h$ die Strecke $\overline{AM}$ auf die Strecke $\overline{CM}$. Da Spiegelungen Abstände erhalten, sind die Abstände der Punkte $A$, $B$ und $C$ von $M$ jeweils gleich. Die Punkte $A,B,C$ liegen also auf einem Kreis mit Mittelpunkt $M$. Diese Argumentation gilt für je zwei der drei Mittelsenkrechten. Folglich schneiden sich alle drei im Mittelpunkt des Umkreises.
qed.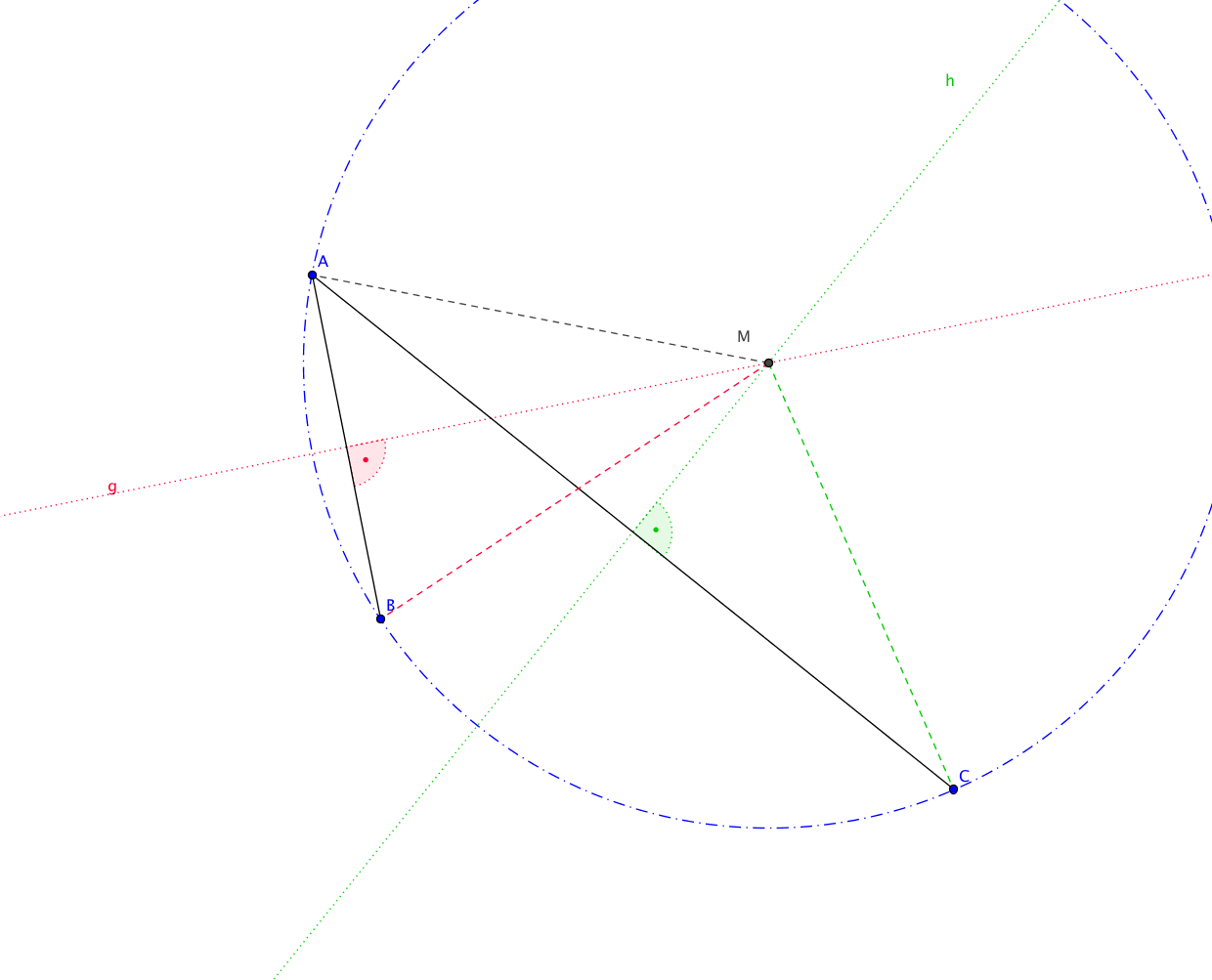
Proposition 3.8. Die Winkelhalbierenden in einem nicht ausgearteten Dreiecks schneiden sich im Mittelpunkt des Inkreises.
Bevor wir in den Beweis einsteigen, eine kleine Vorüberlegung: Gegeben ein Punkt $X$ auf der Winkelhalbierenden $w$ zweier Strahlen $s$ und $t$. Fällen wir das Lot von $X$ auf den Strahl $s$, so ist der Aufpunkt $L(X)$ derjenige Punkt des Strahls, der den kürzesten Abstand von $X$ besitzt. Folglich berührt der Kreis um $X$ mit Radius $|XL(X)|$ den Strahl $s$ einzig in $L(X)$. Spiegeln wir $s$ an der Winkelhalbierenden $w$, so erhalten wir den Strahl $t$. Dementsprechend liefert das Lot von $X$ auf den Strahl $t$ den Punkt auf $t$ mit kürzestem Abstand zum gegebenen Punkt $X$. Der Aufpunkt des Lots von $X$ auf den Strahl $t$ ist das Spiegelbild von $L(X)$ unter der Spiegelung $s_w$. Somit sind die Punkte auf der Winkelhalbierenden der Strahlen $s$ und $t$ charakterisiert durch die Eigenschaft: Ein Punkt $X$ auf $w$ besitzt gleichen Abstand zu $s$ wie zu $t$.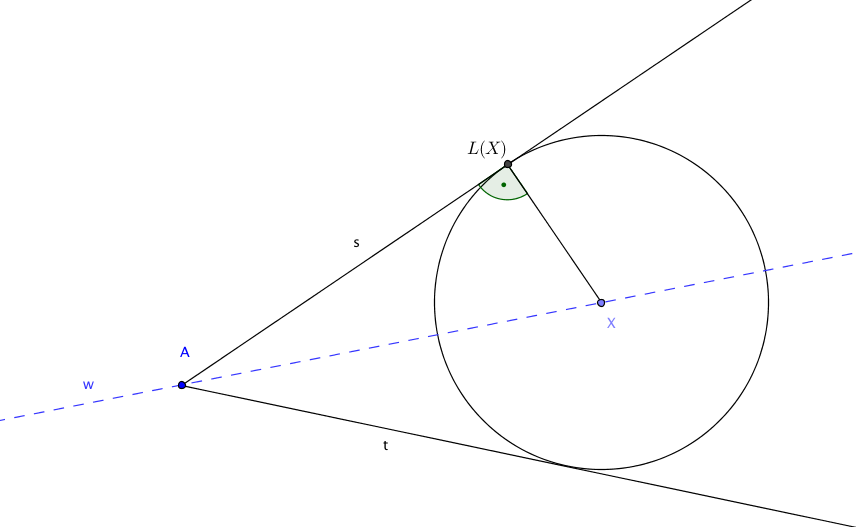
Beweis. Es seien $g$ und $h$ die Winkelhalbierenden zweier der drei Winkel, sagen wir von $\angle {CAB}$ und $\angle{ABC}$. Wären $g$ und $h$ parallel, so wären die beiden Winkel jeweils $180°$, die Winkelsumme im Dreieck widersprechend. Somit schneiden sich die Geraden $g$ und $h$ in einem Punkt $M$. Der Abstand des Punktes $M$ zu den Geraden $AB$, $BC$ und $CA$ ist nach unserer Vorüberlegung jeweils der gleiche. Bezeichnen $Aa$, $Bb$ und $Cc$ jeweils das Lot von $M$ auf die Geraden $BC$, $CA$ und $AB$, so ist $M$ also der Mittelpunkt des Kreises durch diese drei Punkte. Dieser Kreis, der sogenannte Inkreis, berührt die drei Seiten des Dreiecks in diesen drei Punkten. Es bleibt zu zeigen, dass die Gerade $MC$ die Winkelhalbierende des Winkels $\angle BCA$ ist. Dazu betrachten wir die Dreiecke $MCAa$ und $MCBb$. Nach Korollar (3.5) sind diese kongruent. Folglich sind die Winkel $\angle MCAa$ und $\angle MCBb$ gleich, wie zu zeigen war.
qed.