Definition. Ein Viereck $ABCD$ heißt Kreisviereck, wenn es einen Kreis gibt, der durch die Punkte $ABCD$ geht.
Kreisvierecke sind dadurch charakterisiert, dass gegenüber liegende Winkel sich jeweils zu $180°$ aufaddieren. Dieses Phänomen soll etwas genauer beleuchtet werden. Gegeben sei ein Kreis und darin eine Sehne $\overline{BD}$, das heißt eine Strecke, deren Endpunkte auf dem Kreis liegen. Nehmen wir einen dritten Punkt $A$ auf dem Kreis, so ist der Winkel $\sphericalangle BAD$ einzig abhängig davon, auf welchem der beiden Kreisbögen, in die der Kreis zerfällt, wenn wir die Punkte $B$ und $D$ entfernen, der Punkt $A$ gewählt wird. Zumindest zeigt uns Geogebra immer dieselbe Zahl an, solange wir die Position der Punkte $B$ und $D$ nicht verändern.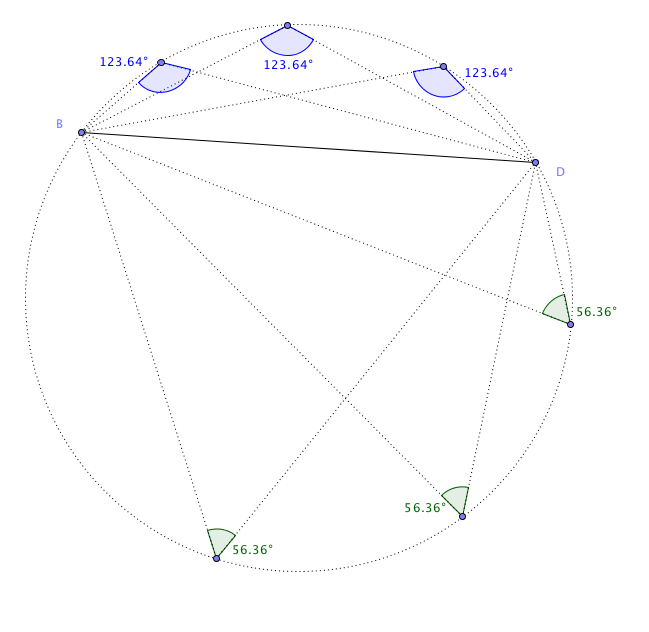
Wir werden später den Satz über Sehnentangentenwinkel beweisen, der zeigt, warum dies sich so verhält. Um diesen Satz zu motivieren, betrachten wir, was passiert, wenn wir den Punkt $A$ auf dem gegebenen Kreisbogen immer näher an den Punkt $D$ heranführen.
Die von $A$ ausgehenden Strahlen in Richtung $B$ und $D$ nähern sich dann den von $D$ ausgehendem Strahl Richtung $B$, sowie dem auf der Tangente im Punkte $D$ liegenden Strahl in Richtung der $A$ gegenüber liegenden Halbebene bezüglich der Geraden $BD$. Während dieser Annäherung ändert sich der Winkel zwischen den beiden jeweils von $A$ ausgehenden Strahlen nicht. Also sollte sich auch der Winkel beim Übergang zu den beiden Grenzwert-Strahlen nicht ändern.
Analog verhält es sich, wenn sich der Punkt $A$ auf dem gegebenen Kreisbogen dem Punkt $B$ nähert.
Satz vom Sehnentangentenwinkel 4.7. Es sei $\overline{BD}$ eine Sehne in einem Kreis und $X\not= B$ ein Punkt auf der Tangente zum Kreis im Punkt $B$. Es sei $A$ ein Punkt auf dem Kreis, der verschieden von $B$ und $D$ ist, und so dass $X$ und $A$ auf verschiedenen Seiten der Gerade $BD$ liegt. Dann gilt $$\sphericalangle XBD=\sphericalangle BAD.$$ 
Beweis. Spiegeln wir an der Mittelsenkrechten der Strecke $\overline{BD}$, so wird der Kreis in sich abgebildet, der Punkt $B$ auf den Punkt $D$ und die Tangente im Punkt $B$ auf die Tangente im Punkt $D$. Bezeichnet $X'$ den Spiegelpunkt von $X$, so gilt für die Winkel $\sphericalangle XBD=\sphericalangle BDX'.$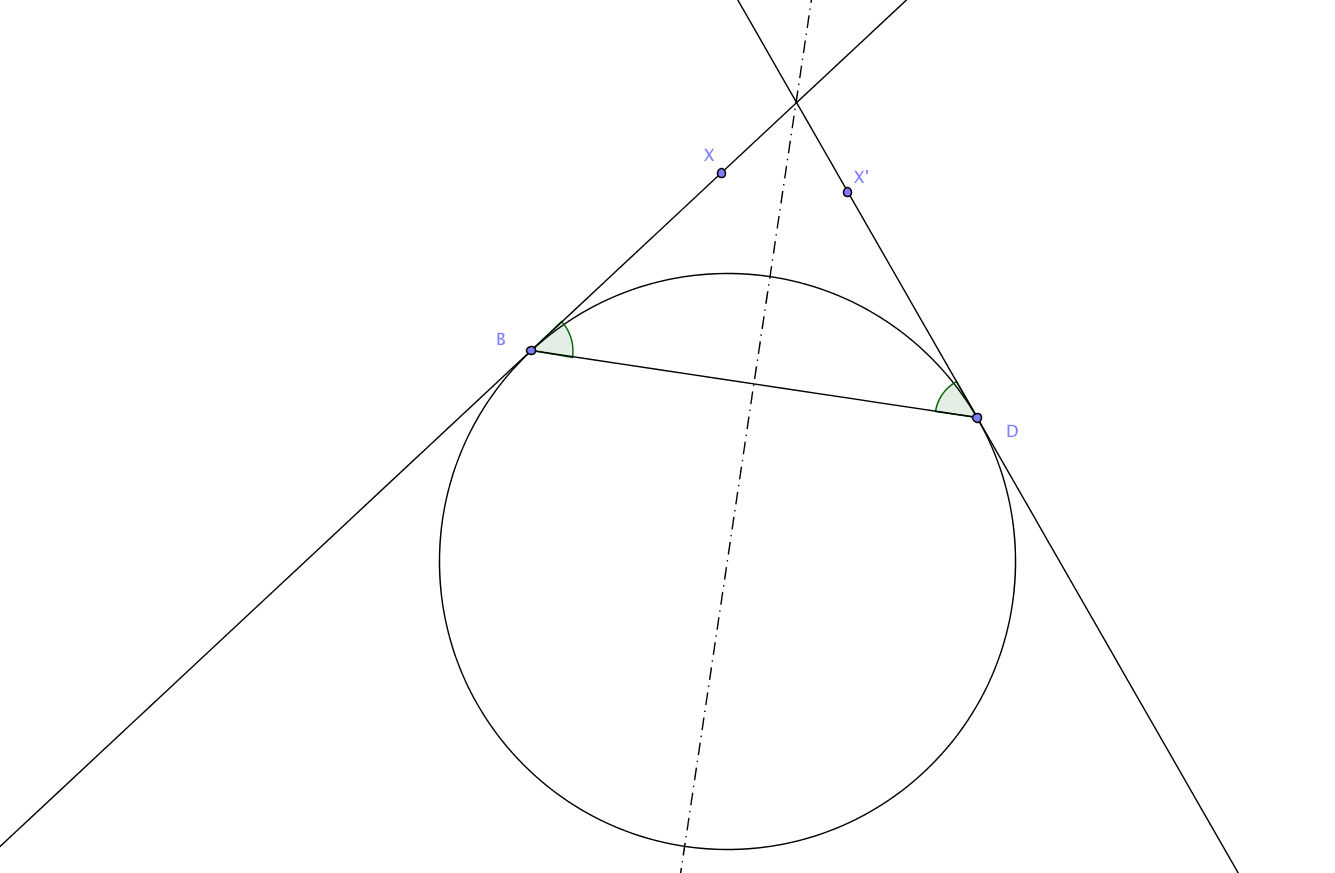
Wir bezeichnen diese beiden Winkel mit $\alpha$. Entsprechend erhalten wir zwei gleiche Winkel $\beta$ zwischen der Geraden $AD$ und den Tangenten im Punkt $A$ und im Punkt $D$, sowie zwei gleiche Winkel $\delta$ zwischen der Geraden $AB$ und den Tangenten im Punkt $A$ und im Punkt $B$.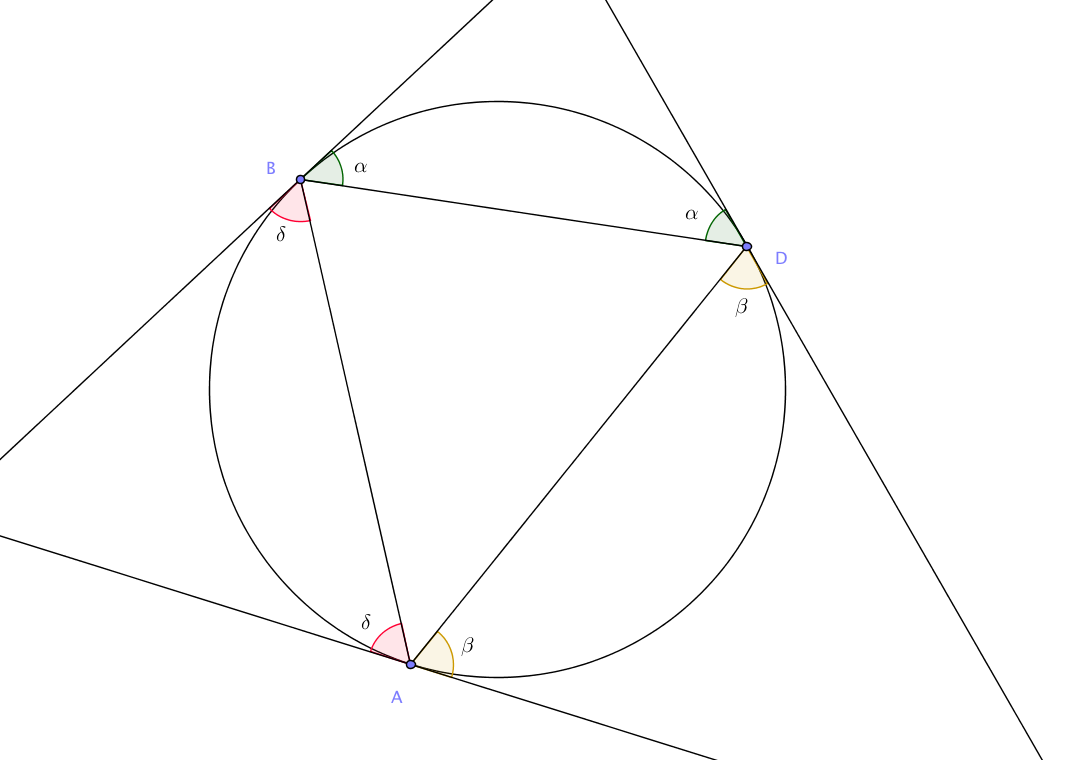
Die Winkel an den einzelnen Punkte $A$, $B$ und $D$ berechnen sich mit den drei Gleichungen \begin{align*}
\sphericalangle DAB&=180°-\beta-\delta\\
\sphericalangle ABD&=180°-\delta-\alpha\\
\sphericalangle BDA&=180°-\alpha-\beta.\\
\end{align*} Addieren wir diese Gleichungen, so erhalten wir als Winkelsumme des Dreiecks $ABD$ $$180°=\sphericalangle DAB+\sphericalangle ABD+\sphericalangle BDA=540°-2\alpha-2\beta-2\delta$$ und folglich $$\alpha+\beta+\delta=180°.$$ Daraus folgt die Behauptung.
qed.
Korollar 4.8. Sind $A$ und $C$ zwei Punkte auf dem Kreis, die auf verschiedenen Seiten der Sehne $\overline{BD}$ liegen. Dann gilt $$\sphericalangle DAB+\sphericalangle BCD= 180°.$$
Beweis. Die den Winkeln $\sphericalangle DAB$ und $\sphericalangle BCD$ entsprechenden Sehnentangentenwinkel am Punkte $B$ addieren sich zu $180°$.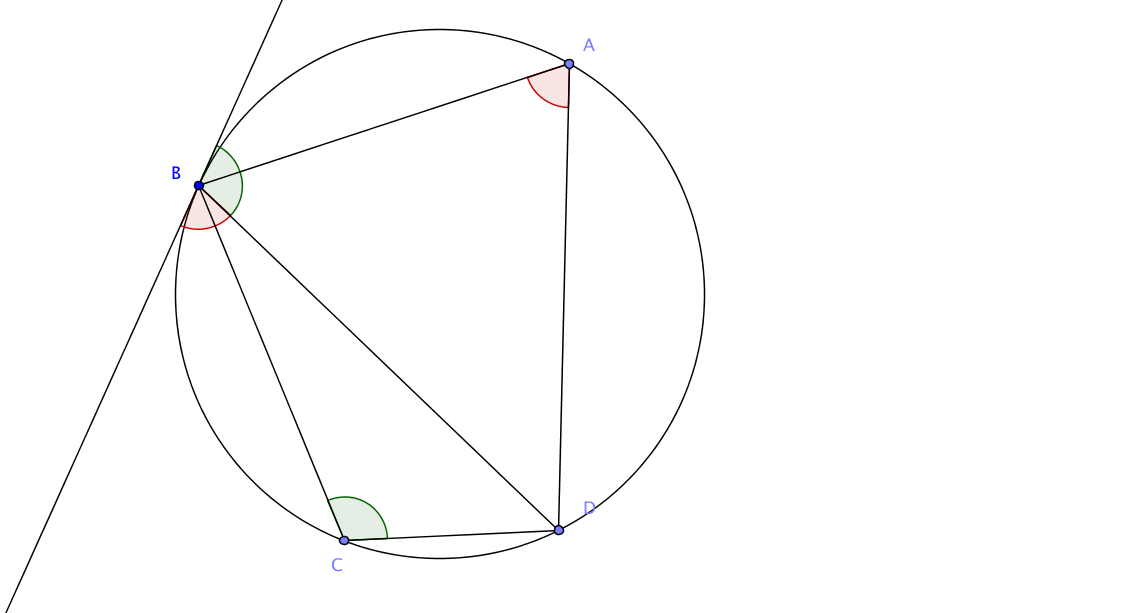
qed.
Jetzt kommen wir zum Beweis des eingangs erwähnten Phänomens, dass zu einer gegebenen Sehne $\overline{BD}$ und einem weiteren Punkt $A$ auf dem Kreis der Winkel $\sphericalangle BAD$ einzig davon abhängt, auf welcher der beiden Kreisbögen der Punkt $A$ liegt.
Peripheriewinkelsatz 4.9. Es sei $\overline{BD}$ eine Sehne im Kreis und $\mathcal B$ einer der beiden Kreisbögen, in die der Kreis zerfällt, wenn wir die Punkte $B$ und $D$ entfernen. Sind $A$ und $C$ zwei Punkte auf dem Kreisbogen $\mathcal B$, so gilt $$\sphericalangle BAD=\sphericalangle BCD.$$ Ist $E$ ein weiterer Punkt auf der gleichen Seite der Geraden $BD$ wie der Bogen $\mathcal B$, für den gilt $$\sphericalangle BAD=\sphericalangle BED,$$ so liegt $E$ auf dem Kreisbogen $\mathcal B$.
Beweis. Beide Winkel in der ersten Aussage sind gleich dem Sehnentangentenwinkel: $$\sphericalangle BAD=\sphericalangle XBD=\sphericalangle BCD.$$ Zur zweiten Aussage betrachten wir zuerst die Winkel $\angle EBD$ und $\angle BDE$. Der Winkel $180°-\angle BED=180°-\angle BAD$ ist wegen Korollar (4.8) gleich den Winkeln der Geraden $BD$ zu den beiden tangentialen Strahlen in $B$ und $D$, welche in die Seite der Geraden $BD$ zeigen, in der der Bogen $\mathcal B$ liegt. Aus der Winkelsumme des Dreiecks $BDE$ folgt $\angle EBD+\angle BDE=180°-\angle BED$. Folglich ist der Winkel $\angle EBD$ kleiner als der Winkel zwischen dem tangentialen Strahl bei $B$ und dem Strahl von $B$ in Richtung $D$. Folglich schneidet der von $B$ ausgehende Strahl in Richtung $E$ den Kreisbogen $\mathcal B$ in einem Punkt $A$. Betrachten wir nun die Dreiecke $BED$ und $BAD$, so sind diese kongruent wegen des Kongruenzsatzes WSW. Außerdem liegt $E$ auf derselben Seite wie $A$. Also muss gelten $A=E$.
qed.
Satz 4.10. Ein Viereck $ABCD$ ist genau dann ein Kreisviereck, wenn die Summe zweier gegenüber liegender geometrischer Winkel gleich $180°$ ist.
Bemerkung. Ein Viereck besitzt immer eine Diagonale, die ganz im Inneren des Vierecks verläuft. Diese Diagonale teilt das Viereck in zwei Dreiecke. Folglich ist die Winkelsumme im Viereck zweimal die Winkelsumme eines Dreiecks, also gleich $360°$. Ist also die Summe eines Paares gegenüber liegender geometrischer Winkel in einem Viereck gleich $180°$, so gilt dies auch für das andere Paar gegenüber liegender Winkel.
Beweis von 4.10. Ist $\overline{BD}$ Diagonale in einem Kreisviereck, so ist diese Diagonale eine Sehne im Kreis und teilt diesen in zwei Kreisbögen. Die Punkte $A$ und $C$ liegen nicht auf demselben Kreisbogen. Nach Korollar (4.8) addieren sich die Winkel bei $A$ und $C$ also zu $180°$.
Nehmen wir nun umgekehrt an, gegenüber liegende Winkel addierten sich zu $180°$. Eine der beiden Diagonalen, sagen wir mal die Diagonale $\overline{BD}$, verläuft, wie wir zu Anfang des Kapitels feststellten, ganz im Inneren des Vierecks. Wir betrachten den Kreis $\mathcal K$, auf dem die drei Punkte $B$, $C$ und $D$ liegen. Der Punkt $A$ muss auf der Seite der Geraden $BD$ liegen, welche $D$ nicht enthält. Jetzt können wir den zweiten Teil des Peripheriewinkelsatzes benutzen. Aus diesem, kombiniert mit (4.8), folgt, dass $A$ auch auf dem Kreis $\mathcal K$ liegen muss.
qed.