Es seien $s$ und $t$ zwei Strahlen in der Ebene mit dem gleichen Anfangspunkt $A$. Man legt ein Ziffernblatt um $A$, das in $360$ gleiche Teile eingeteilt ist. Die Ziffern mögen entgegengesetzt dem
Uhzeigersinn wachsen.
Es sei $x(s) \in \mathbb{R}$ die Ziffer, wo der Strahl $s$ liegt und $x(t) \in \mathbb{R}$ die Ziffer, wo der Strahl $t$ liegt. Dann ist $x(s) - x(t)$ der Drehwinkel zwischen $s$ und $t$:
\[
\sphericalangle(s,t) = x(s) - x(t)
\] 
Diese Zahl ist anschaulich die Größe der Drehung, die den Strahl $t$ entgegengesetzt dem Uhrzeigersinn auf den Strahl $s$ dreht [1].
Eine volle Umdrehung von einem der Strahlen $s$ oder $t$ ändert den Winkel nicht. Deshalb werden bei Drehwinkeln die folgenden Größen als gleich angesehen:
\[
\ldots, \alpha - 2\cdot 360,\; \alpha - 360, \; \alpha, \; \alpha +
360, \; \alpha + 2\cdot 360, \ldots
\] So bezeichnen die folgenden Zahlen den gleichen Drehwinkel:
\[
-50,\; 310, \; 670.
\] Wir schreiben $-50^{\circ} = 310^{\circ} = 670^{\circ}$ und sagen zum Beispiel $310$ Grad. Man sagt auch, Gradrechnung ist Rechnen modulo $360$.
Diese Konvention hat den Vorteil, dass für drei Strahlen, die von dem Punkt $A$ ausgehen, die folgende Summen- oder Kürzungsregel gilt:
\[\label{Wkl0e}
\sphericalangle (r,s) + \sphericalangle (s,t) = \sphericalangle (r,t).
\] Steht in so einer Winkelsumme derselbe Strahl (hier der Strahl $s$) einmal auf der linken und einmal auf der rechten Seite, so kann er gekürzt werden. Insbesondere folgt daraus:
\[
\sphericalangle (s,t) + \sphericalangle (t,s) = 0^{\circ}.
\] Es sei $-s$ der Strahl mit dem gleichen Anfangspunkt wie $s$, aber mit entgegengesetzter Richtung. Die Vereinigung der Strahlen $s$ und $-s$ ist eine Gerade $g$. Offensichtlich gilt:
\begin{equation}
\sphericalangle (s, -s) = 180^{\circ}
\end{equation} In diesem Fall sprechen wir von einem gestreckten Winkel. Aus der Summen- oder Kürzungsregel für Drehwinkel und der Definition eines gestreckten Winkels folgt
\begin{align*}\sphericalangle(s,t)&=\sphericalangle(s,-s)+\sphericalangle(-s,t)\\&=\sphericalangle(s,-s)+\sphericalangle(-s,-t)+\sphericalangle(-t,t)\\&=\sphericalangle(-s,-t)+360\text{°}\\&=\sphericalangle(-s,-t).\end{align*} Die resultierende Gleichung \[
\sphericalangle(s,t)=\sphericalangle(-s,-t)\] besagt, dass Wechselwinkel (manche sagen auch Gegenwinkel) gleich sind.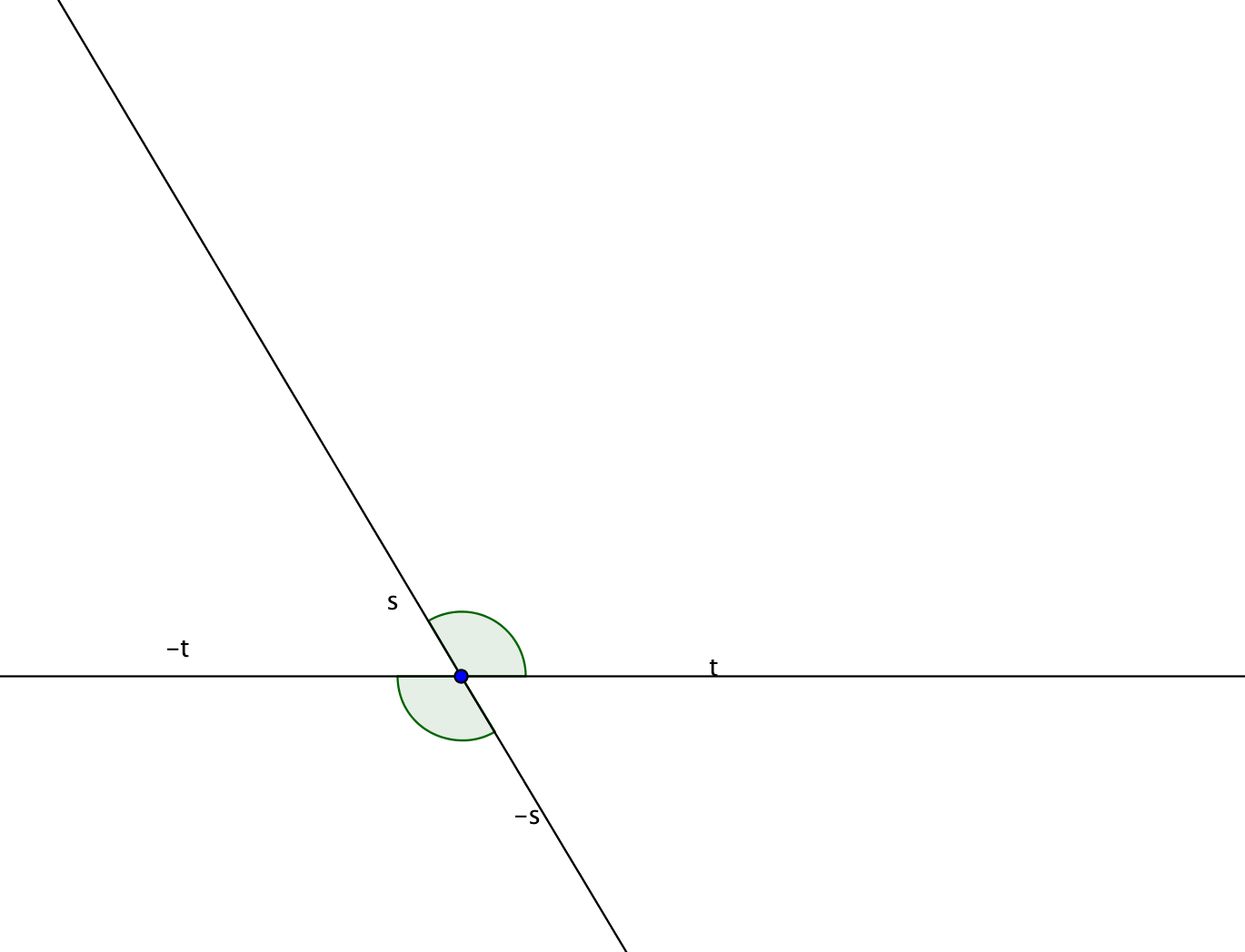
Wir sagen, zwei Strahlen $s$ und $t$ mit dem gleichen Anfangspunkt stehen senkrecht aufeinander (oder sind orthogonal), wenn gilt
\[
\sphericalangle (s,t) = 90^{\circ} \quad \text{oder} \quad
\sphericalangle (s,t) = - 90^{\circ}.
\] Dies heisst, $s$ halbiert den gestreckten Winkel $(t,-t)$, also $
\sphericalangle (s,t) = \sphericalangle (-t,s).
$ Man sieht, dass $s$ und $t$ genau dann orthogonal sind, wenn $s$ und $-t$ es sind. Es macht also Sinn, von orthogonalen Geraden zu reden.
Neben dem Drehwinkel betrachtet man auch den geometrischen Winkel zweier Strahlen $s$ und $t$ mit gleichem Anfangspunkt $A$. Es gibt genau eine Zahl $\alpha$, so dass $0 \leq \alpha \lt 360$ und $
\sphericalangle (s,t) = \alpha
$ gilt. Der geometrische Winkel $\angle(s,t)$ ist eine Zahl zwischen $0$ und $180$. Er ist definiert durch die Vorschrift: \begin{array}{ccc}
\angle(s,t) = \alpha, & \text{wenn} & 0 \leq \alpha \leq 180 \\
\angle(s,t) = 360 - \alpha, & \text{wenn} & 180 \leq \alpha
\end{array} Geometrische Winkel kennen keine Drehrichtung:
\[ \angle(s,t) = \angle(t,s).\] Anders als Drehwinkel, lassen sich geometrische Winkel nicht eindeutig addieren: Gilt $\angle(s,t)=30°$ und $\angle(t,u)=40°$, so kann einerseits gelten $\angle(s,u)=70°$, andererseits aber auch $\angle(s,u)=10°$.
Notation. Es seien $A,B,C$ drei Punkte. Es sei $t$ der Strahl mit dem Anfang $B$ in Richtung $A$ und es sei $s$ der Strahl mit dem Anfang $B$ in Richtung $C$. Dann schreiben wir [2]: \[
\sphericalangle ABC = \sphericalangle (s,t) \quad \text{und} \quad
\angle ABC = \angle (s,t).\]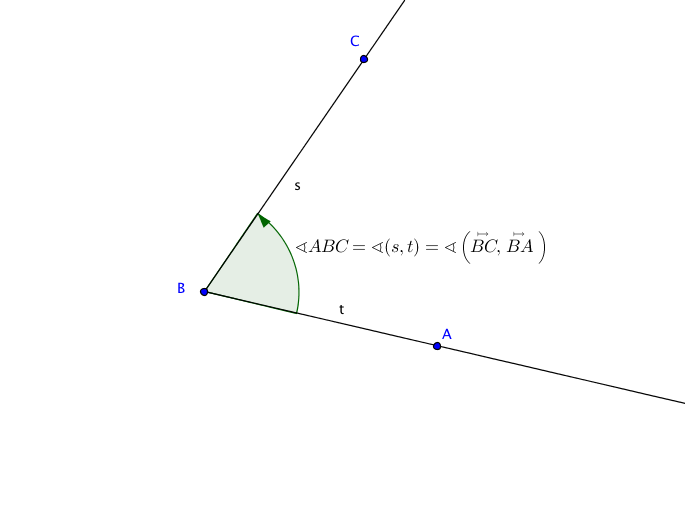
Definition. Es sei $M$ ein Punkt in der Ebene $\mathbb{E}$ und $r > 0$ eine reelle Zahl. Der Kreis $\mathcal{K}$ mit dem Mittelpunkt $M$ und dem Radius $r$ besteht aus allen Punkten $A \in \mathbb{E}$, die Abstand $r$ von $M$ haben. In Formeln ausgedrückt: \[
\mathcal{K} = \{A \in \mathbb{E} \; | \; |AM| = r \}.\]
Prinzip 1.3. Es seien $A$, $B$, $C$ paarweise verschiedene Punkte in der Ebene. Dann gibt es entweder einen Kreis oder eine Gerade auf dem diese drei Punkte liegen. Zwei Kreise durch die Punkte $A$, $B$, $C$ sind notwendig gleich.
Insbesondere schneiden sich verschiedene zwei Kreise bzw. ein Kreis und eine Gerade höhstens in zwei Punkten.
Satz. Es seien $\mathcal{K}_1$ und $\mathcal{K}_2$ Kreise mit Mittelpunkten $M_1, M_2$ und Radien $r_1$ und $r_2$. Wir nehmen an, dass $r_1 \leq r_2$ gilt. Schneiden sich die beiden Kreise, so gelten die beiden Ungleichungen $$r_2 - r_1 \le |M_1M_2| \le r_1 + r_2.$$
Bemerkung. Es gilt auch die Umkehrung des Satzes: Gelten beide obigen Ungleichungen, so schneiden sich die beiden Kreise.
Beweis des Satzes. Es sei $S$ ein Schnittpunkt.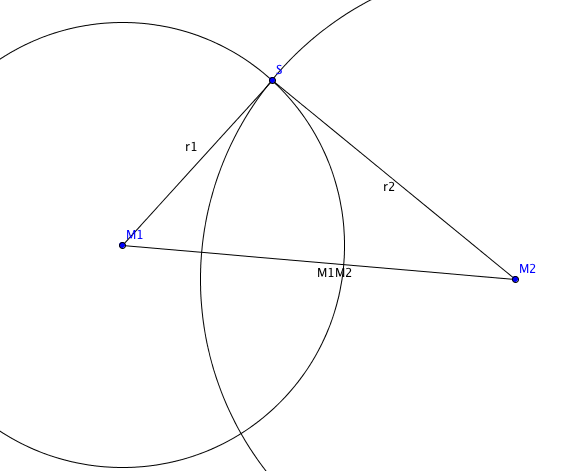 
Die Dreiecks-Ungleichung besagt : $$|M_{1}M_{2}|\leq |M_{1}S|+|SM_{2}|= r_{1}+r_{2},$$ sowie $$r_{2}= |M_{2}S|\leq |M_{2}M_{1}|+|M_{1}S|= |M_{1}M_{2}|+r_{1}.
$$ Bringen wir $r_{1}$ auf die linke Seite, so erhalten wir die Ungleichung $$r_{2}-r_{1}\leq|M_{1}M_{2}|.$$ Zu kären bleiben noch die Fälle, wo Gleichheit gilt.
Gilt im ersten Fall in der Dreiecksungleichung $$|M_{1}M_{2}|\leq|M_{1}S|+|SM_{2}|=r_{1}+r_{2}$$ Gleichheit, so liegt $S$ auf der Strecke $\overline{M_{1}M_{2}}$. Die beiden Kreise berühren sich in $S$.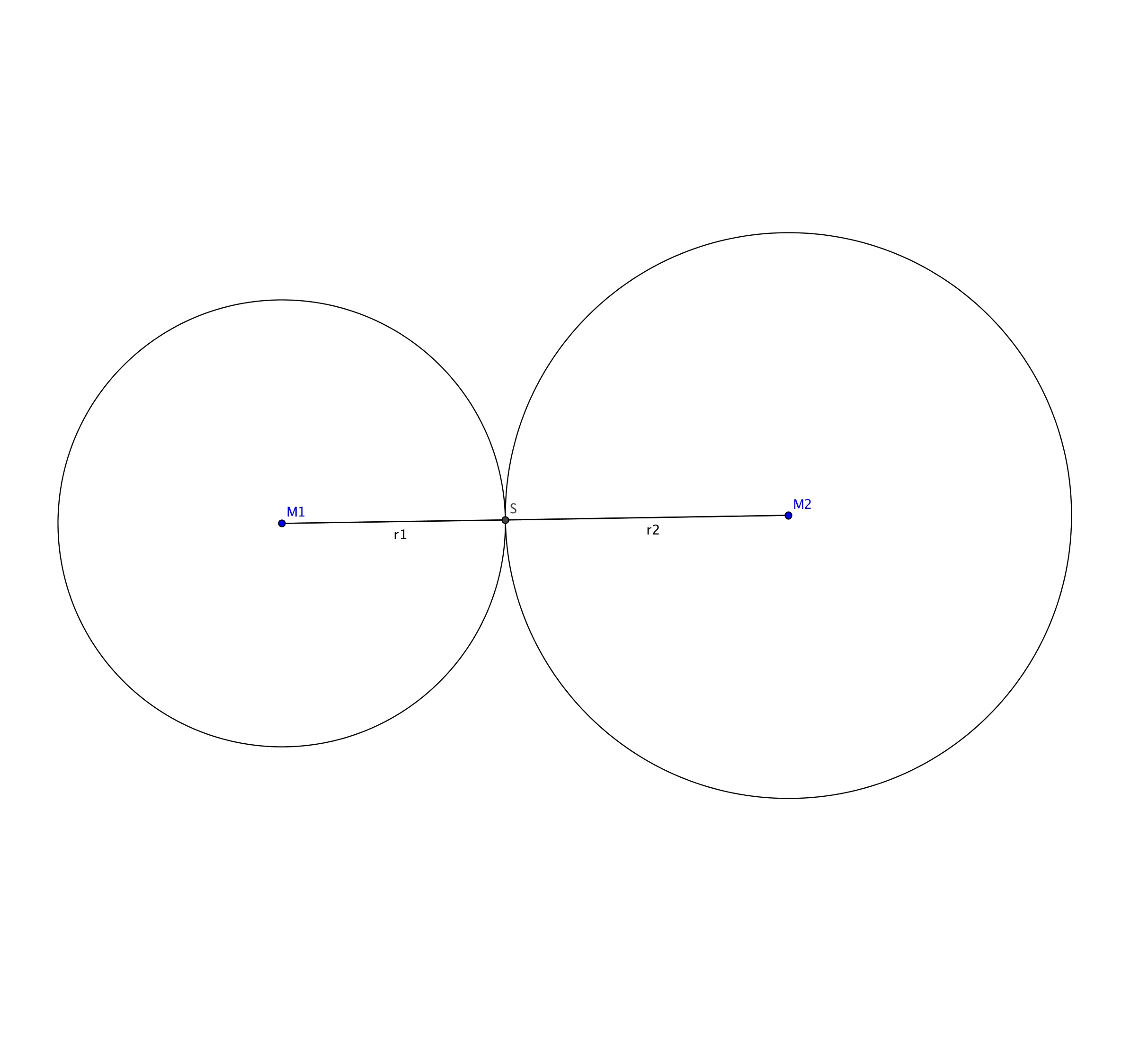
Gilt im zweiten Fall die Gleichheit $$r_{2}=|M_{2}S|=|M_{2}M_{1}|+|M_{1}S|=|M_{1}M_{2}|+r_{1},$$ so liegt $M_{1}$ auf der Strecke $\overline{M_{2}S}$. Die beiden Kreise liegen ineinander und berühren sich.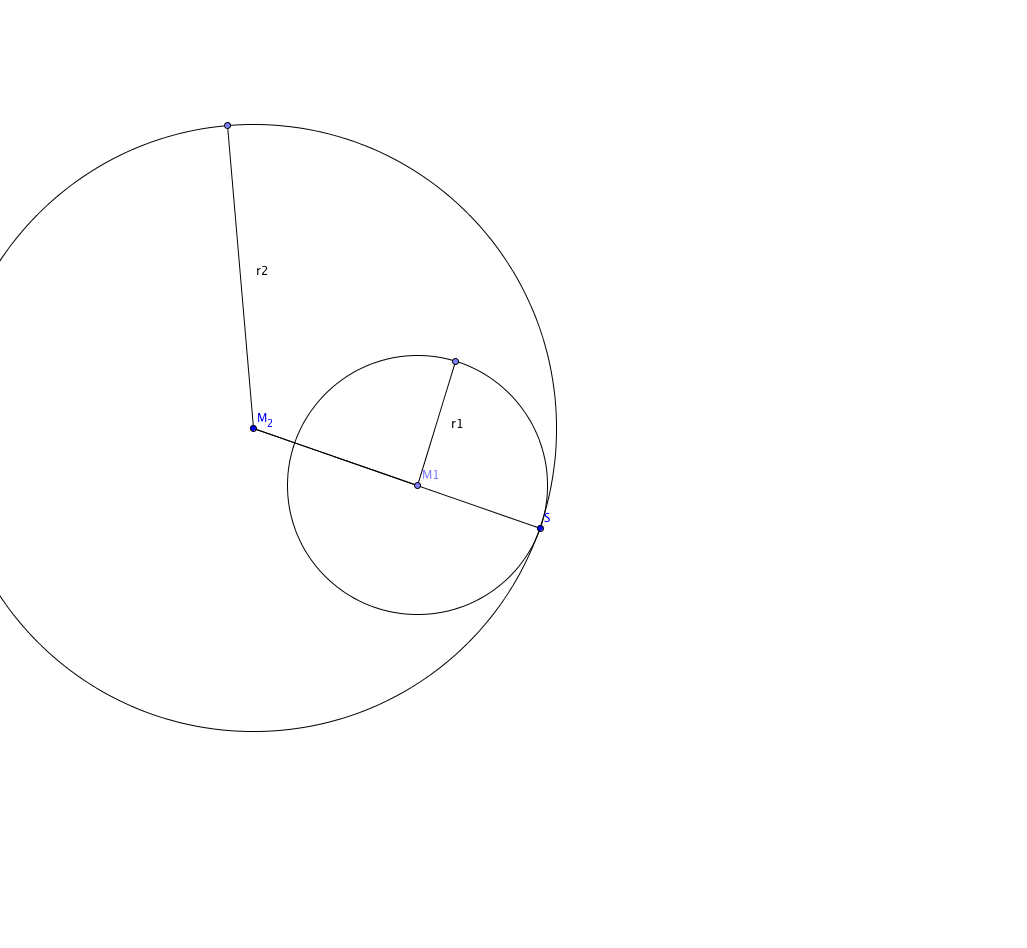 
Wir haben nicht gezeigt, dass es im Falle einer echten Ungleichung tatsächlich noch einen zweiten Schnittpunkt gibt. Anschaulich ist dies klar: Gilt keine Gleichheit, so gilt in der Dreiecksungleichung nicht die Gleichheit. Folglich liegen die drei Punkte $S$, $M_1$ und $M_2$ nicht auf einer Geraden. Wenn wir entlang der von $M_1$ und $M_2$ aufgespannten Geraden spiegel, wird der Schnittpunkt $S$ auf einen zweiten Schnittpunkt abgebildet. Spiegelungen und Drehungen werden im nächsten Kapitel der Vorlesung besprochen.
--------
[1] Diese Konvention wurde nachträglich geändert, um Konsistenz innerhalb der Vorlesung zu erreichen. Sie stimmt nicht überein mit der Konvention auf Seite 3 des Skripts von Herrn Zink. Leider ist das Skript von Herrn Zink in dieser Hinsicht inkonsistent: Auf Seite 7, Zeile 7 wird der Drehwinkel $\alpha=\sphericalangle\left(s,D(s)\right)$ anders definiert als in Definition 20 auf Seite 15. Dort steht $\vartheta(\phi)=\sphericalangle\left(\phi(s),s\right)$. In der ersten Formel wird die Drehung auf den zweiten Eintrag angewandt, in der zweiten Formel auf den ersten Eintrag.
Die in dieser Vorlesung angewandte Konvention ist die obige, konsistent mit Definition 20 im Skript von Herrn Zink.
[2] Was $\sphericalangle ABC$ bedeutet hat sich nicht verändert. Die Beschreibung als Drehwinkel zwischen Strahlen wurde der Konvention entsprechend angepasst. Ein Bild wurde hinzugefügt.