Zweiter Strahlensatz 5.4. Es seien $g$ und $g'$ zwei nicht parallele Geraden. Es sei $p: g \rightarrow g'$ eine Parallelprojektion entlang der Geraden $h$. Es seien $A, B, C, D \in g$ vier paarweise verschiedene Punkte. Wir setzen $p(A) = A'$, $p(B) = B'$, $p(C) = C'$, $p(D) = D'$ und $T_A =
\overset{\longrightarrow}{AA'}$, $T_B =
\overset{\longrightarrow}{BB'}$, $T_C =
\overset{\longrightarrow}{CC'}$, $T_D =
\overset{\longrightarrow}{DD'}$. Dann gilt:
$$
\frac{T_A - T_B}{T_C - T_D} =
\frac{\overrightarrow{AB}}{\overrightarrow{CD}}
$$
Beweis. Es sei $q: g \rightarrow h$ die Parallelprojektion entlang $g'$. Wir bezeichnen $q(A)=A''$, $q(B)=B''$, $q(C)=C''$ und $q(D)=D''$.
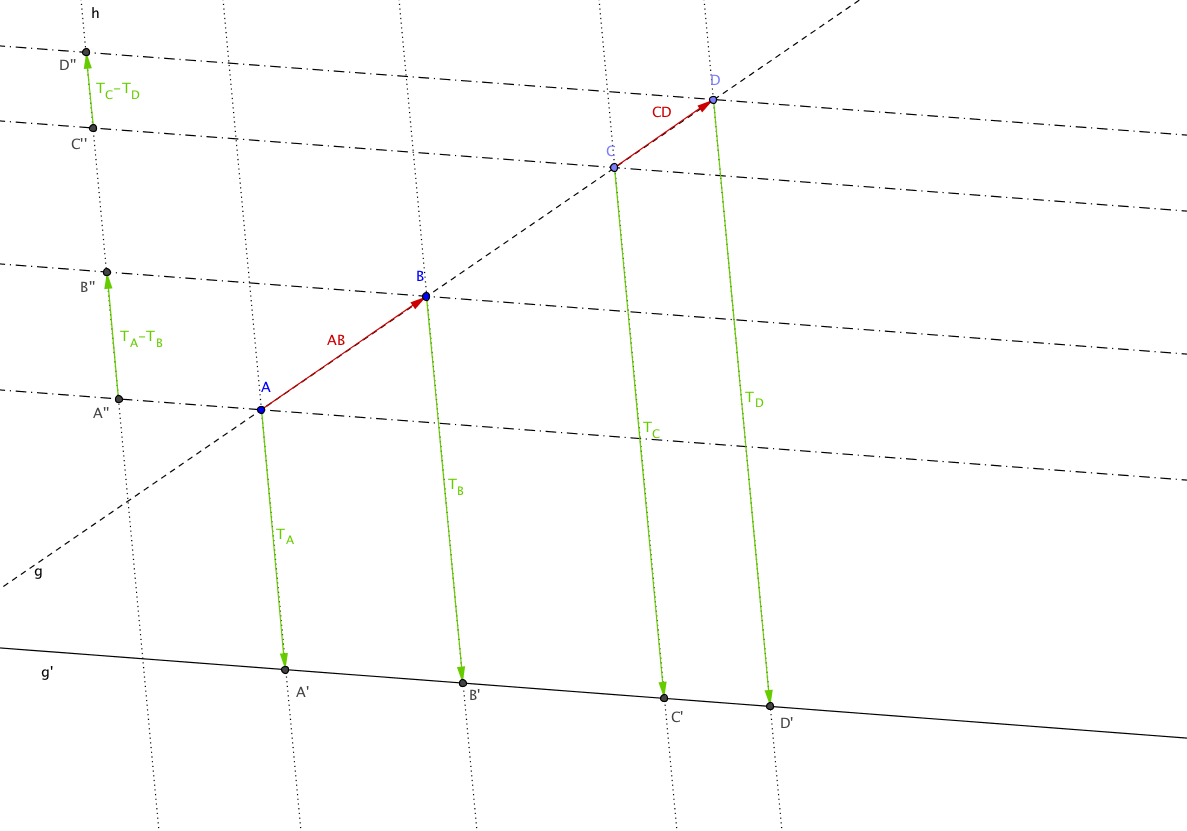
Es gilt
$$
\overset{\longrightarrow}{A''B''} = T_A - T_B \quad \text{und}
\quad \overset{\longrightarrow}{C''D''} = T_C - T_D
$$ und folglich $$ \frac{T_A - T_B}{T_C - T_D}=\frac{\overrightarrow{A''B''}}{\overrightarrow{C''D''}} .$$ Anwendung des ersten Strahlensatzes auf die Parallelprojektion $q$ liefert
$$
\frac{\overrightarrow{A''B''}}{\overrightarrow{C''D''}}=\frac{\overrightarrow{AB}}{\overrightarrow{CD}} .$$qed.
Oft wird der zweite Strahlensatz auch im Spezialfall formuliert, in dem $A =A'$ der Schnittpunkt der beiden Geraden ist. Daraus lässt übrigens sich die obige allgemeinere Formulierung herleiten.
Korollar 5.5. Es seien $g$ und $g'$ zwei nicht parallele Geraden, die sich in einem Punkt $A$ schneiden. Es sei $p: g \rightarrow g'$ eine Parallelprojektion. Es seien $B, D \in g$ zwei von $A$ verschiedene Punkte. Wir setzen $p(B) = B'$ und $p(D)=D'$. Dann gilt $$
\frac{\overrightarrow{BB'}}{\overrightarrow{DD'}}
= \frac{\overrightarrow{AB}}{\overrightarrow{AD}}
$$ 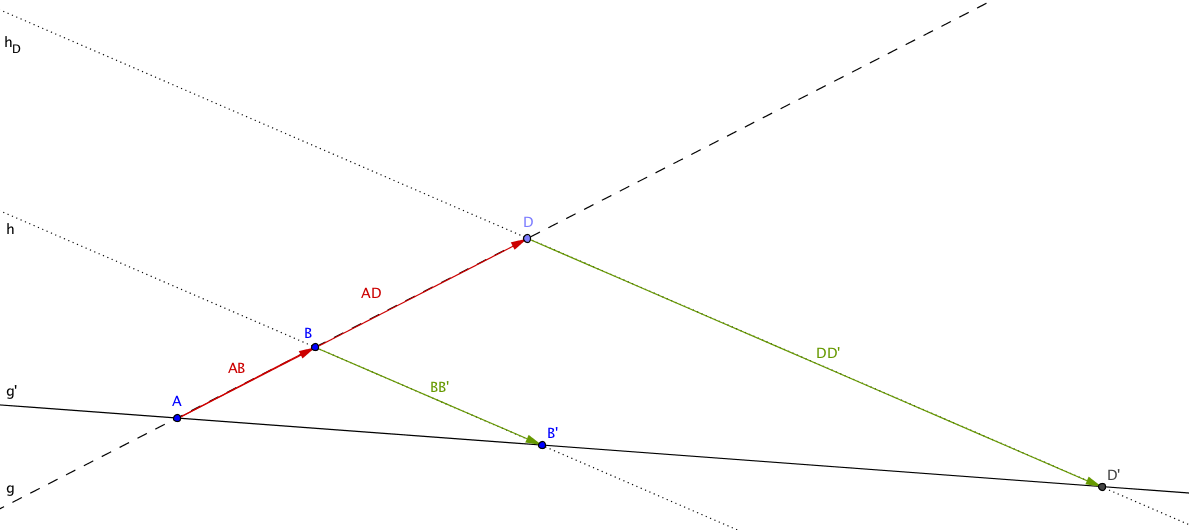
Beweis. Wir setzen im zweiten Strahlensatz $A=A'=C=C'$. Dann gilt $T_A=T_C=0$. Mit $T_B =
\overset{\longrightarrow}{BB'}$ und $T_D =
\overset{\longrightarrow}{DD'}$ folgt die Aussage unmittelbar.
qed.