Satz 2.5. Es sei $\phi$ eine Bewegung der Ebene $\mathbb{E}$ und $X \in\mathbb{E}$ ein Punkt. Wenn die Punkte $X$, $\phi(X)$, und $\phi^2(X)$ nicht auf einer Geraden liegen, so ist $\phi $ eine Drehung. Der Fixpunkt von $\phi$ ist der Mittelpunkt des Kreises $\mathcal{K}$ durch $X, \phi(X)$, und $\phi^2(X)$. 
Beweis. Der Mittelpunkt des Kreises sei $Z$. Da $|ZX| =
|Z\phi(X)|$ gibt es eine Drehung $\theta$, so dass $\theta(X) =\phi(X)$ und $\theta(Z) = Z$. Wir wollen beweisen, dass $\theta = \phi$.
Es sei $d = |X\phi(X)|$. Da $\theta$ und $\phi$ Isometrien sind folgt:\[
d = |\phi(X) \phi^2(X)| = |\phi(X) \theta(\phi(X))|\] Es sei $\mathcal{D}$ der Kreis um $\phi (X)$ mit dem Radius $d$. Da sich zwei verschiedene Kreise höchstens in zwei Punkte schneiden, finden wir
\[ \theta(\phi(X)) \in \mathcal{K} \cap \mathcal{D} = \{X, \phi^2(X) \}.
\] Falls gilt $\theta(\phi(X)) = \phi^2(X)$, so überführt $\theta$ die Strecke $\overline{X\phi(X)}$ in die Strecke $\overline{\phi(X)\phi^2(X)}$ und daher stimmen die Bewegung $\phi$ und die Drehung $\theta$ überein. 
Der zweite Fall $\theta(\phi(X)) = X$ kann nicht auftreten, denn sonst wäre $\theta$ die Punktspieglung an dem Mittelpunkt der Strecke $X\phi(X)$. Da $Z$ ein Fixpunkt von $\theta $ ist, wäre $Z$ der Mittelpunkt der Strecke $X\phi(X)$. Damit hat der Kreis $\mathcal{D}$ den Radius $d/2$. Wir finden \[
|Z\phi(X)| + |Z\phi^2(X)| = (d/2) + (d/2) = |X\phi(X)| = |\phi(X)\phi^2(X)|.
\] Aus dieser Gleichung folgt, dass $Z$ ein Punkt der Strecke $\overline{\phi(X)\phi^2(X)}$ ist. Also lägen im zweiten Fall die Punkte $X$ und $\phi^2(X)$ auf der Geraden $Z\phi(X)$. Das ist ein Widerspruch zur der Voraussetzung, dass die Punkte $X$, $\phi(X)$ und $\phi^2(X)$ nicht auf einer Geraden liegen.
qed. 
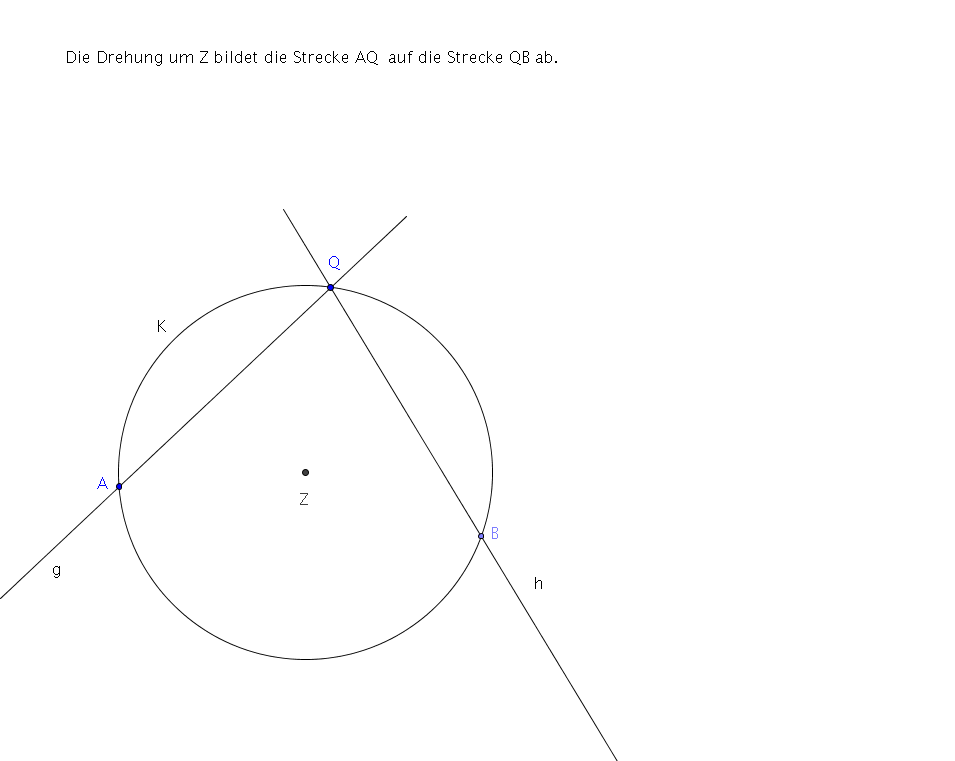
Korollar 2.6. Sei $\phi$ eine Bewegung und sei $g$ eine Gerade, so dass sich $\phi(g)$ und $g$ genau in einem Punkt schneiden. Dann ist $\phi$ eine Drehung.
Beweis. Sei $\phi(g) = h$ und $Q = g \cap h$. Ist $Q$ Fixpunkt, so ist nichts zu beweisen. Ansonsten gibt es Punkte $A \in g$ und $B \in h$, die beide von $Q$ verschieden sind, mit $
\phi(A) = Q$ und $ \phi(Q) = B$. Nun lässt sich der obige Satz anwenden.
qed.