Eine Bewegung $T$ ist genau dann eine Translation, falls ein Strahl $s$ in der Ebene existiert mit $T(s)\subset s$. Die benutzen wir im Beweis der folgenden, etwas technisch anmutenden Aussage.
Proposition 2.13. Sei $\phi$ eine Bewegung und $T$ eine Translation. Dann ist $\phi\circ T\circ\phi^{-1}$ ebenfalls eine Translation.
Beweis. Sei $s$ Strahl mit $T(s)\subset s$ gegeben. Dann ist auch $t=\phi(s)$ ein Strahl. Wegen der Gleichungskette $$\phi\circ T\circ\phi^{-1}(t)=\phi\circ T(s)\subset\phi(s)=t$$ bildet die Bewegung $\phi\circ T\circ\phi^{-1}$ den Strahl $t$ in sich ab, ist folglich Translation.
qed.
Satz 2.14. Es sei $Z\in\mathbb{E}$ ein vorgegebener Punkt der Ebene. Jede Bewegung $\phi:\mathbb{E}\rightarrow\mathbb{E}$ lässt sich eindeutig als Komposition $\phi=D\circ T$ einer Translation $T$ und einer Drehung $D$ mit Zentrum $Z$ schreiben. Sie lässt sich ebenfalls eindeutig als Komposition $\phi=T'\circ D$ derselben Drehung $D$ und einer Translation $T'$ schreiben.
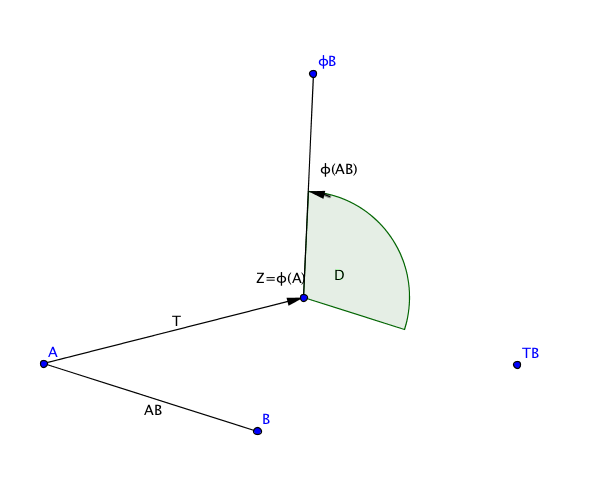
Beweis. Sei $A=\phi^{-1}(Z)$ und $T=\overset{\rightarrow}{AZ}$. Für einen Punkt $B\not=A$ der Ebene gilt dann: $$|ZT(B)|=|T(A)T(B)|=|AB|=|\phi(A)\phi(B)|=|Z\phi(B)|.$$ Also gibt es eine Drehung $D$ um $Z$ mit $D\left(T(B)\right)=\phi(B)$. Derart bildet $D\circ T$ die Strecke $\overline{AB}$ auf die Strecke $\overline{Z\phi(B)}$ ab. Das zugrundeliegende Prinzip (2.1) der Bewegung liefert $D\circ T=\phi$. Die Eindeutigkeit ist klar. Man kann auch schreiben $$D\circ T=(D\circ T\circ D^{-1})\circ D=T'\circ D.$$ Nach der obigen Proposition (2.13) steht in der Klammer eine Translation.
qed.