Spiegelungen

Neben den Bewegungen betrachten wir weitere Isometrien, die Spiegelungen. Sie gehorchen folgendem Prinzip.

Prinzip 2.16. Es sei $g$ eine Gerade in der Ebene $\mathbb{E}$ und $H^{+} , H^{-}$ die beiden durch sie bestimmten Halbebenen. Die Spiegelung an der Geraden $g$ ist eine Isometrie $$s_{g}:\mathbb{E}\rightarrow\mathbb{E}$$ der Ebene mit folgenden Eigenschaften:

1. $s_{g}(P)=P$ für alle $P\in g$.
2. $s_{g}(H^{+})=H^{-}$ und $s_{g}(H^{-})=H^{+}$.
3. Für je zwei Strahlen $t_{1}$ und $t_{2}$ gilt $\sphericalangle(s_{g}(t_{1}),s_{g}(t_{2}))=-\sphericalangle(t_{1},t_{2})$.

Anders als die Drehwinkel erhaltenden Bewegungen, kehren Spiegelungen das Vorzeichen von Drehwinkeln um. Das entspricht der allmorgendlichen Erfahrung im Badezimmer. Das Spiegelbild einer Linksdrehung ist eine Rechtsdrehung. Als Isometrie erhält eine Spiegelung Abstände von Punkte $$|PQ|=|s_{g}(P)s_{g}(Q)|.$$ Wie jede Isometrie, bilden Spiegelungen Strecken, Strahlen, Geraden und Kreise auf ebensolche Strecken, Strahlen, Geraden und Kreise ab. Liegt insbesondere der Mittelpunkt $M$ eines Kreises $\mathcal{K}$ auf der Geraden $g$, so ist dieser Mittelpunkt fixiert unter der Spiegelung $s_g$. Folglich ist der Kreis $ \mathcal{K}$ invariant $s_{g}(\mathcal{K})=\mathcal{K}$ unter der Spiegelung.

Gegeben ein Punkt in der Ebene, lässt sich sein Spiegelpunkt unter der Spiegelung $s_g$ an der Geraden $g$ leicht konstruieren. Sei $P\in H^{+}$, so wählen wir zwei beliebige Punkte $M_{1},M_{2}$ auf der Geraden $g$ und zeichnen Kreise $\mathcal{K}_{1}$ und $\mathcal{K}_{2}$ durch $P$ mit Mittelpunkten $M_{1}$ und $M_{2}$. Die Kreise sind unter der Spiegelung $s_{g}$ invariant. Folglich ist $s_{g}(P)$ ebenfalls Schnittpunkt von $\mathcal{K}_{1}$ und $\mathcal{K}_{2}$. Die Punkte $P$ und $s_{g}(P)$ liegen in verschiedenen Halbebenen und sind die einzigen Schnittpunkte der beiden Kreise $\mathcal{K}_{1}$ und $\mathcal{K}_{2}$. Also ist $s_{g}(P)$ der zweite Schnittpunkt dieser Kreise. Beginnt man mit $Q=s_{g}(P)$, so folgt aus Konstruktion: $$s_{g}^{2}:=s_{g}\circ s_{g}=\mathrm{id}.$$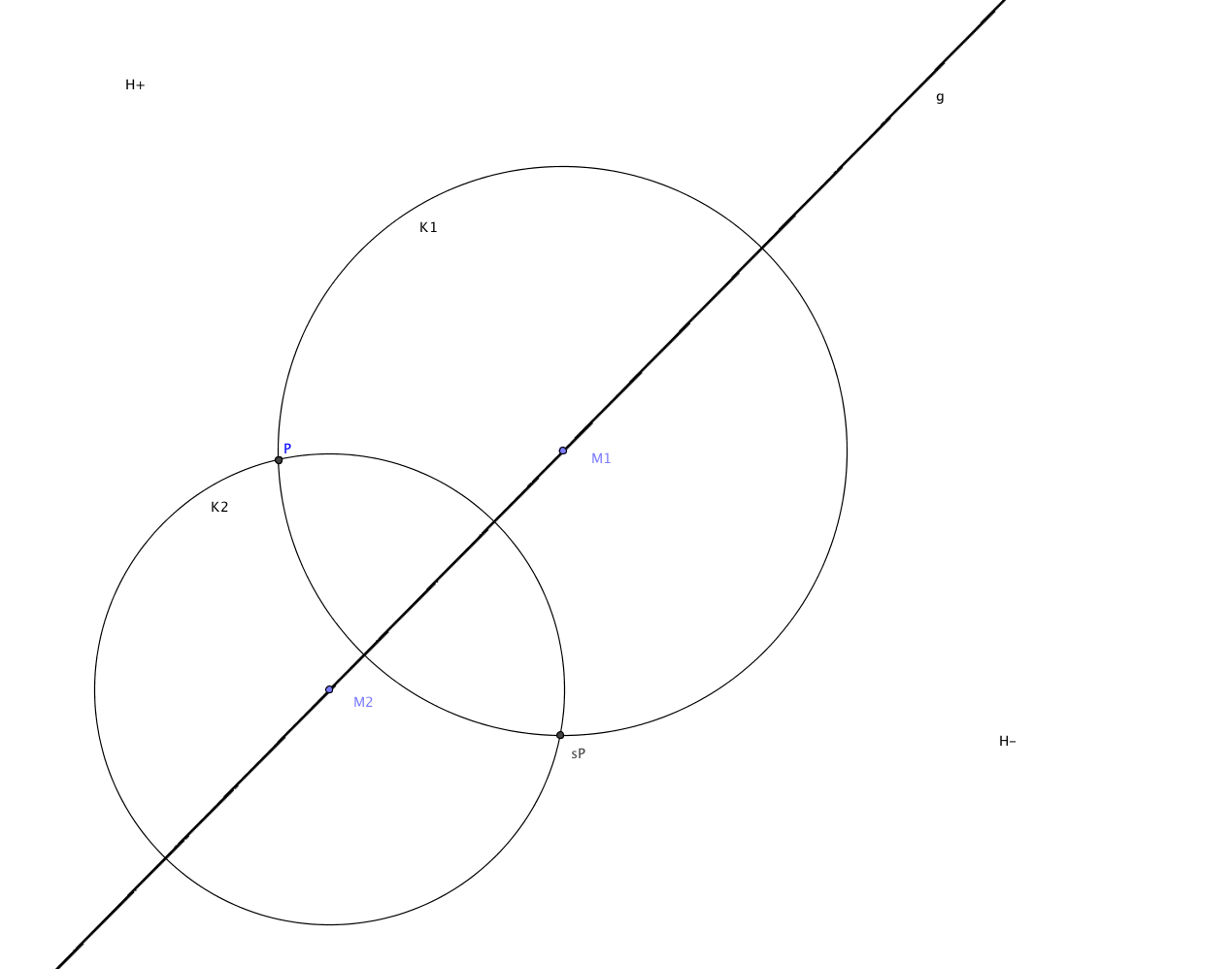

Lemma. Ist $P\notin g$, so ist die unter der Spiegelung $s_g$ invariante Gerade $Ps_{g}(P)$ orthogonal zu $g$.

Beweis. Sei $F$ der Schnittpunkt von $Ps_{g}(P$) und $g$ und $u$ der von $F$ ausgehende Strahl Richtung $P$. Dann ist $-u$ der von $F$ ausgehende Strahl Richtung $s_{g}(P)$. Sei $t$ ein auf der Spiegelgeraden $g$ Strahl mit Anfang $F$. Da Spiegelungen das Vorzeichen von Drehwinkel umkehrt, gilt $$
\sphericalangle(u,t)=-\sphericalangle(s_{g}(u),s_{g}(t))=-\sphericalangle(-u,t).
$$ Mit der Gleichung $$\sphericalangle(-u,u)=\sphericalangle(-u,t)+\sphericalangle(t,u)=180^{0}$$ erhält man $$\sphericalangle(u,t)=-180^{0}+\sphericalangle(t,u)$$ und mit $\sphericalangle(t,u)=-\sphericalangle(u,t)$ ergibt sich $$2\sphericalangle(u,t)=180^{0}.$$ Also sind $u$ und $t$ orthogonal, der geometrische Winkel ist $90^{0}$.
qed.