Definition. Unter einer beseiteten Strecke $\overline{AB}$ verstehen wir eine Strecke mit einem gewählten Anfangspunkt und einer gewählten Halbebene zur Geraden $AB$.
Eine beseitete Strecke fixiert bei einer Strecke also einen Anfangspunkt und damit eine Richtung, nämlich die zum anderen Ende. Darüber hinaus ist sie politisch voreingenommen: Sie favorisiert entweder die linke oder aber die rechte Seite. Wir können das bildlich darstellen, indem wir die Strecke mit einer Pfeilspitze versehen, um den Anfangs- vom Endpunkt zu unterscheiden, sowie einem Schatten, um die favorisierte Seite zu kennzeichnen.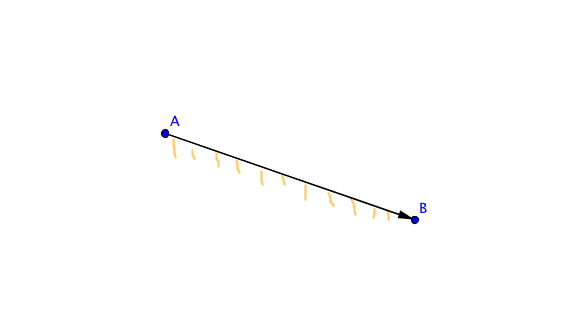
Eine Spiegelung an der Geraden $AB$ ändert einzig den Schatten: Er fällt dann auf die andere Seite.
Satz 2.17. Es seien $\overline{AB}$ und $\overline{CD}$ zwei beseitete Strecken gleicher Länge. Dann gibt es genau eine Isometrie $\sigma$, die die beseitete Strecke $ \overline{AB}$ auf die beseitete Strecke $\overline{CD}$ abbildet.
Beweis. Entsprechend dem Prinzip (2.1) gibt es eine eindeutige Bewegung $\phi$ mit $\phi(A)=C$ und $\phi(B)=D$. Respektiert $\phi$ die gewählten Seiten der Geraden $g=AB$ und $h=CD$, so ist $\phi=\sigma$. Andernfalls respektiert $\phi\circ s_{g}=s_{h}\circ\phi$ die gewählten Seiten dieser Geraden.
qed.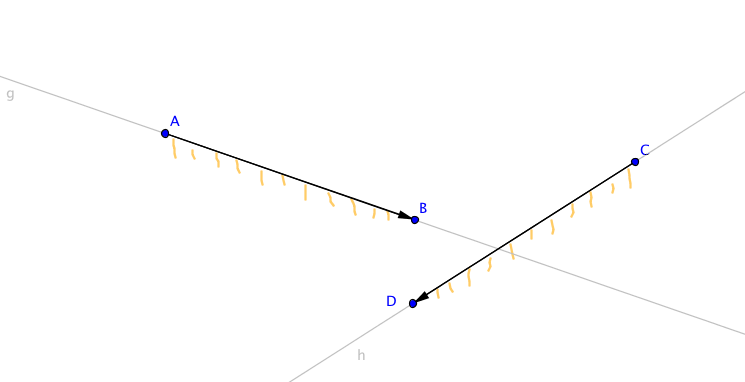
Definition. Eine Isometrie nennt man orientierungserhaltend, wenn sie eine Bewegung ist. Ansonsten nennt man sie orientierungsumkehrend.
Für eine Isometrie $\sigma$ setzt man:\begin{array}{lrr}
\mathrm{or}(\sigma)=&1 & \mbox{wenn}\;\sigma\;\mbox{eine Bewegung ist,}\\
\mathrm{or}(\sigma)=&-1 & \mbox{wenn}\;\sigma\;\mbox{keine Bewegung ist.}
\end{array}
Mit dieser Notation gilt also für Strahlen $s,t$ die Formel $$\sphericalangle\left(\sigma(s),\sigma(t)\right)=\mathrm{or}(\sigma)\cdot\sphericalangle\left(s,t\right).$$ Aus dieser Formel folgt für je zwei Isometrien $\sigma$ und $\tau$ $$\mathrm{or}(\sigma\circ\tau)=\mathrm{or}(\sigma)\cdot\mathrm{or}(\tau).$$