Satz von Hjemslev 2.20. Sei $\phi$ eine Bewegung der Ebene und $g$ eine Gerade. Dann liegen die Mittelpunkte aller Strecken $\overline{P\phi(P)}$ für Punkte $P\in g$ auf einer Geraden.
Beweis. Statt der Bewegung $\phi$ betrachten wir die Komposition $\tau=\phi\circ s_g$. Für Punkte $P$ auf der Geraden $g$ gilt wegen $P=s_g(P)$ die Gleichung $\phi(P)=\tau(P)$. Nach Satz (2.19) ist $\tau$ eine Gleitspiegelung mit Achse $m$. Nach der dritten Aussage von Satz (2.18) liegen die Mittelpunkte der Strecken $\overline{P\phi(P)}$ für Punkte $P\in g$ auf der Achse $m$ der Gleitspiegelung $\tau$.
qed.
Die Achse $g$ einer Gleitspiegelung $\tau=T\circ s_g$ lässt sich im Allgemeinen einfach konstruieren: Gegeben zwei Punkte $A$ und $B$ in der Ebene und ihre Bildpunkte $\tau(A)$ und $\tau(B)$, so konstruiere man die Mittelpunkte $A'$ und $B'$ der Strecken $\overline{A\tau(A)}$ und $\overline{B\tau(B)}$. Sind $A'$ und $B'$ verschieden, so ist die Verbindungsgerade notwendigerweise die Achse $g$ der Gleitspiegelung. Die Translation $T$ erhält man, indem man von $A$ und $\tau(A)$ jeweils das Lot auf $g$ fällt.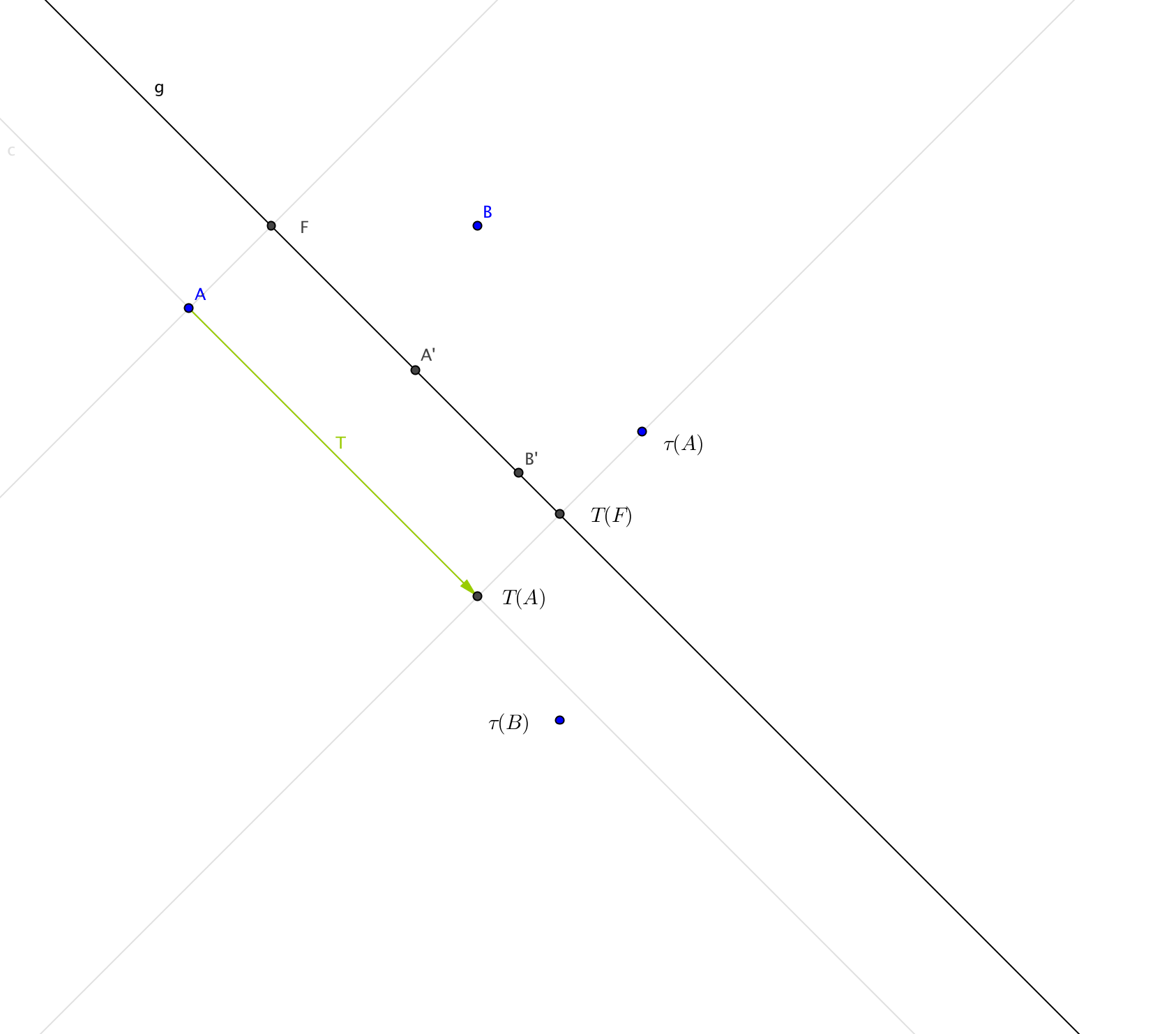
Ein Problem hat man, sollten die Mittelpunkte $A'$ und $B'$ zusammenfallen, denn dann findet sich keine eindeutig bestimmte Gerade durch die beiden Punkte. Ist es wirklich ein Problem? Dazu ein kleiner Satz.
Proposition 2.21. Es sei $\tau$ eine Gleitspiegelung und es seien $A_1, \ldots,A_n$ Punkte in der Ebene, so dass die Mittelpunkte der Strecken $\overline{A_k\tau(A_k)}$ für alle $k$ mit $1\leq k\leq n$ in einem Punkt $M$ zusammenfallen. Dann liegen alle Punkte $A_k$ auf einer Geraden $h$. Die Achse $g$ der Gleitspiegelung $\tau$ steht senkrecht zu $h$ und geht durch $M$.
Beweis. Es sei $\tau=T\circ s_g$. Wir nennen den Punkt $A_1$ vorübergehend $P$. Dann rekapitulieren wir die Konstruktion im Beweis der dritten Aussage in Proposition (2.18). 
Liegt $P$ zufällig auf der Achse $g$, so bezeichnen wir mit $h$ die Senkrechte zu $g$ durch $P$. Ansonsten sei $h$ die Gerade $Ps_g(P)$ und $F$ der Punkt, in dem sich $h$ und $g$ senkrecht schneiden. Es sei $M$ der Mittelpunkt der Strecke $\overline{F\tau(F)}$ und $D_M$ die Punktspiegelung mit Zentrum $M$. In dieser Situation gilt, so wurde gezeigt, die folgende Gleichheit von Isometrien $$\tau=D_M\circ s_h.$$ Die Gleitspiegelung $\tau$ lässt sich also als Spiegelung an $h$, gefolgt von einer Punktspiegelung $D_M$ mit Zentrum $M$ darstellen. Wir wenden $D_M$ auf diese Gleichung an und erhalten $$D_M\circ\tau=D_M\circ D_M\circ s_h=s_h.$$ Wir wenden dies nun an auf die in der Proposition geschilderte Situation: Für jedes $k$ ist $M$ der Mittelpunkt der Strecke $\overline{A_k\tau(A_k)}$ und folglich gilt $$A_k=D_M\circ \tau(A_k)=s_h\left(A_k\right).$$ Damit ist jedes $A_k$ ein Fixpunkt der Spiegelung $s_h$ und liegt deshalb auf $h$. Damit ist die Proposition bewiesen.
qed.
Wir können diese Proposition benutzen, um die Achse der Gleitspiegelung aus den Bildern $\tau(A)$ und $\tau(B)$ auch dann zu konstruieren, wenn die Mittelpunkte $A'$ und $B'$ der Strecken $\overline{A\tau(A)}$ und $\overline{B\tau(B)}$ gleich sind. Dann ist $h=AB$ und wir bekommen $g$, indem wir die Senkrechte zu $h$ konstruieren, die durch den Punkt $M=A'=B'$ geht. Die Translation $T$ erhält man wie zuvor, indem man von $A$ und $\tau(A)$ jeweils das Lot auf $g$ fällt. 