Für eine Gerade $g$ bezeichne $s_g$ die Spiegelung an dieser Gerade. Das Spiegelbild eines Punktes $A$, der nicht auf der Geraden $g$ liegt, sit der Punkt $A'=s_g(A)$, der auf einer Senkrechten zur Spiegelachse durch $A$ liegt. Die Strecke $\overline{AA'}$ wird duch die Spiegelachse halbiert. Schneiden sich eine Gerade $AB$ durch zwei Punkte $A$ und $B$ und die gespiegelte Gerade $A'B'$, so ist der Durchschnitt invariant unter der Spiegelung und damit ein Fixpunkt der Spiegelung. Gibt es keinen Schnittpunkt, sind also $AB$ und $A'B'$ parallel, so haben sie keinen Schnittpunkt mit der Spiegelachse, sind parallel zu $g$.
Seien $A,B$ auf derselben Seite der Geraden $g$ und $A',B'$ die Spiegelbilder. Die Strecken $AB'$ und $A'B$ werden ineinander gespiegelt und schneiden sich auf der Spiegelachse. Geometrische Winkel bleiben bei Spiegelungen erhalten.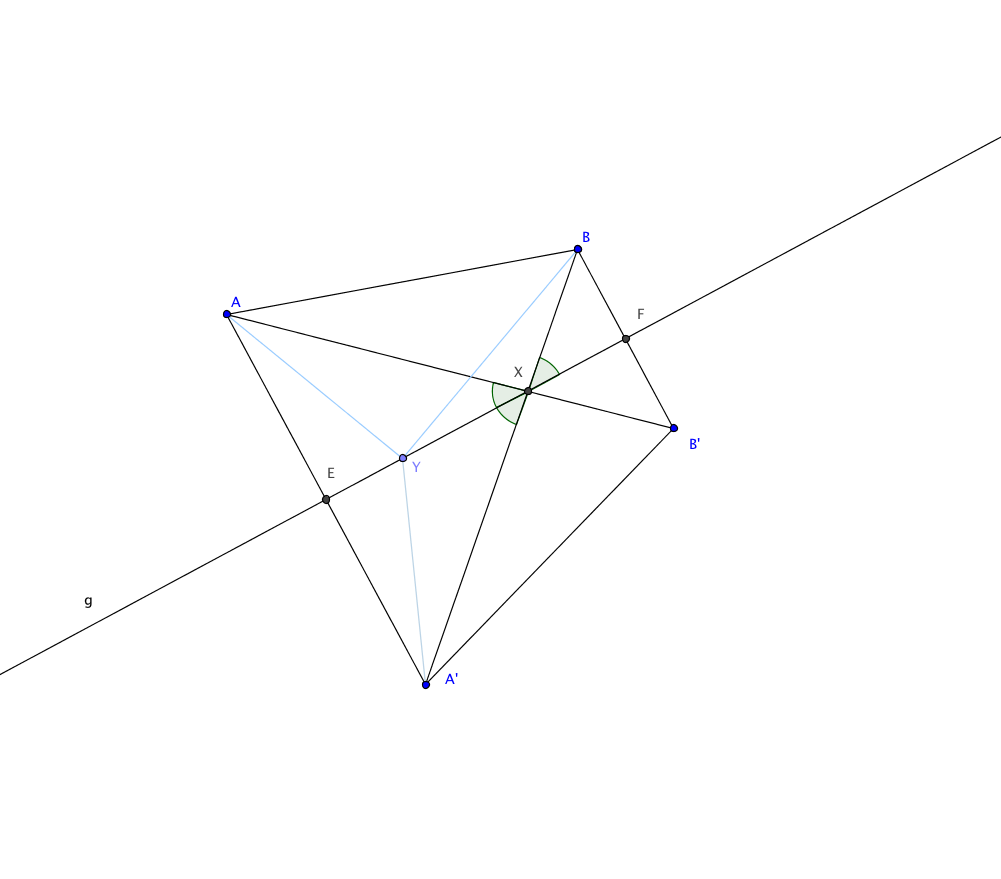
In der Skizze ist der geometrische Winkel $\angle AXE$ deshalb gleich dem gespiegelten Winkel $\angle A'XE$ und dieser wiederum gleich dem Gegenwinkel $\angle BXF$. Insgesamt gilt also $$\angle AXE=\angle BXF.$$ Der kürzeste Weg von einem Punkt $A$ zur Spiegelachse und dann zu einem Punkt $B$ auf derselben Seite der Spiegelachse ist der Streckenzug $AXB$. Denn für jeden anderen Punkt $Y$ auf der Spiegelachse wäre der zurückgelegte Weg $|AY|+|YB|$ länger als die Strecke $$|A'B|=|AX|+|XB|.$$
In der Physik sagt man, der an einem Spiegel gespiegelte Lichtstrahl von einem Punkt $A$ zu einem Punkt $B$ nimmt den kürzesten Weg. Einfallswinkel und Ausfallswinkel sind gleich.