Wir betrachten nun die Komposition zweier Spiegelungen $s_g$ und $s_h$ für Geraden $g$ und $h$. Es können zwei Fälle auftreten: Die Geraden sind entweder parallel oder sie schneiden sich. Wir wollen diese beiden Fälle separat betrachten.
1. Fall: Die Geraden $g$ und $h$ schneiden sich im Punkt $P$.
Seien $g^{+}$ und $h^{+}$ Strahlen in $g$ und $h$ mit Anfangspunkt $P$. Wir bezeichnen mit $$\alpha=\sphericalangle\left(g^{+},h^{+}\right)$$ den Drehwinkel der Drehung, welche den Strahl $h^+$ in den Strahl $g^+$ überführt.
Eine andere Wahl der Strahlen liefert $\alpha'=\sphericalangle\left(g^{+},h^{-}\right)=\alpha+180°$. Es gilt $$s_{g}\circ s_{h}=D(P,2\alpha)=D(P,2\alpha')=D(P,\alpha)^{2}.$$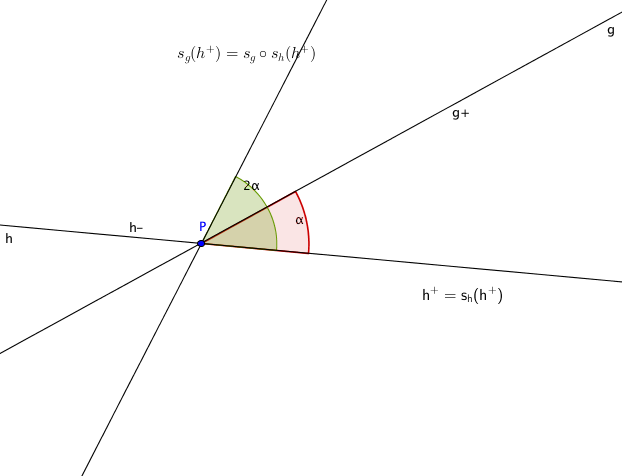
Beweis. Die Komposition zweier orientierungsumkehrender Spiegelungen ist eine orientierungserhaltende Bewegung $\phi$. Der Punkt $P$ wird von beiden Spiegelungen $s_h$ und $s_g$ fixiert. Damit hat $\phi$ einen Fixpunkt, ist also eine Drehung um den Punkt $P$. Den Winkel können wir erkennen, indem wir das Bild des Strahles $h^+$ berechnen: Durch die erste Abbildung $s_h$ wird dieser Strahl in sich abgebildet. Der Winkel berechnet sich wie folgt: \begin{array}{rcl}
\sphericalangle\left(s_g(h^{+}),h^{+}\right)& = & \sphericalangle\left(s_g(h^{+}),g^{+}\right)+\sphericalangle\left(g^{+}),h^{+}\right)\\
& = & \sphericalangle\left(s_g(h^{+}),s_g(g^{+})\right)+\sphericalangle\left(g^{+},h^{+}\right) \\
& = & -\sphericalangle\left(h^{+},g^{+}\right)+\sphericalangle\left(g^{+},h^{+}\right) \\
& = & 2\sphericalangle\left(g^{+},h^{+}\right)\\
&=& 2\alpha
\end{array} Die Gleichungen benutzen der Reihe nach die Additionsformel für Drehwinkel, die Invarianz der Geraden $g$ unter der Spiegelung $s_g$, die Umkehrung der Drehwinkel durch die Spiegelung $s_g$, Umkehrung des Vorzeichens bei Vertauschen von Quell- und Zielstrahl, und die Definition von $\alpha$.
qed.
2. Fall: Die Geraden $g$ und $h$ sind parallel.
Sei $k$ eine zu $g$ und $h$ senkrechte Gerade und seien $G=g\cap k$ und $H=h\cap k$ die jeweiligen Schnittpunkte. Bezeichnet $T$ die Translation $T=\overset{\rightarrow}{GH}$, so gilt $$s_{h}\circ s_{g}=T\circ T=2T.$$
Beweis. Die Komposition zweier orientierungsumkehrender Spiegelungen ist eine orientierungserhaltende Bewegung $s_{h}\circ s_{g}=\phi$. Die Gerade $k$ und alle ihre Parallelen sind invariant unter beiden Spiegelungen. Folglich sind all diese parallelen Geraden invariant unter der Bewegung $\phi$. Da unter den Bewegungen nur eine Translation parallele invariante Geraden zulässt, muss es sich bei $\phi$ um eine Translation handeln. Um den Verschiebungsvektor zu identifizieren, reicht es, die Verschiebung eines Punktes zu berechnen. Wir nehmen dazu den Punkt $G$. Unter der ersten Spiegelung $s_g$ bleibt $G$ fix. Unter der zweiten Spiegelung an der Geraden $h$ wird $G=s_g(G)$ am Punkt $H$ gespiegelt, also um $2T$ verschoben.
qed.